Collatzův problém
Zajímavá úloha z teorie čísel může mít velmi hezké počítačové zpracování.
Na úvod - jde o úlohu známou také jako Ulamův problém nebo Syrakuský problém. Algoritmus jejího výpočtu je velmi jednoduchý, ale stále chybí matematický důkaz. Jedná se o posloupnost vytvořenou výpočtem z libovolného přirozeného čísla. Pokud je číslo sudé, dělíme jej dvěma. Jestliže je liché, vynásobíme ho třemi a přičteme jedna. Nakonec vždy dojdeme k číslu jedna.
Na úloze je krásné, že její počítačové zpracování je poměrně jednoduché a přehledné. Lze jej zapsat v tabulkovém kalkulátoru pro offline prezentaci nebo v nějakém webovém provedení. Velmi názorně zapojuje práci s podmínkami i cykly. (V odkazu pod článkem ukazuji výpočet pomocí PHP.)
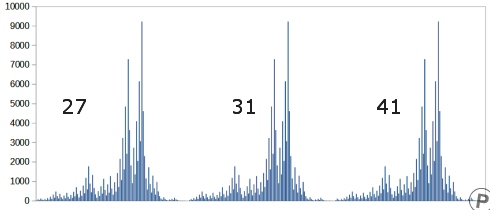
Na ukázku jsem vykreslil (LibreOffice Calc) do jednoho grafu výpočty z čísel 27, 31 a 41. Proč právě tato? Počet cyklů je přibližně stejný (více než 100 operací) a nejvyšší dosažené hodnoty rovněž. (Pro zajímavost: číslo 29 potřebuje pouze 18 výpočtů s nejvyšší hodnotou 88.) K zamyšlení je určitě i podobnost všech tří grafů.

Pozoruhodné je, že je velmi obtížné odhadnout, které číslo vede k vyššímu počtu početních operací a jaká bude maximální hodnota při výpočtu celé posloupnosti. Tato otázka ostatně bývá lákavější než vlastní důkaz. Proč? Pokud totiž dojde ke grafickému zpracování pomocí nějakého vykreslovacího programu, dostáváme zajímavé výsledky, které připomínají fraktály. Je zajímavé si potom položit úlohu do jiného směru, zda lze i zde předpokládat nějakou soběpodobnost jako u fraktálové geometrie?
>>>>>
09-09-2014