Tečna ke křivce v Geogebře
Další použití skvělého prostředí u funkcí.
Jakkoli se může zdát, že Geogebra je platforma především pro geometrii, já ji mnohem častěji a také raději používám pro funkce. Vysvětlit a názorně prezentovat jejich vlastnosti je v Geogebře neuvěřitelně snadné. Patří sem také derivace funkce včetně geometrické aplikace. Například pro zobrazení tečny ke křivce v bodě. Pro učitele jde o excelentní výukový materiál, pro žáky o možnost otestovat se, jak problematice rozumí.
Ve videu v odkazu pod článkem ukazuji tři funkce a možnosti tečny. Vlastní úloha je v podobě souboru vhodná pro výklad i zkoušení. Velká přidaná hodnota je v dynamičnosti, protože jednoduchou změnou parametru dosahujeme různé výstupy. Výpočet derivace funkce i derivace v bodě je velmi snadný, neboť jej má Geogebra v nabídce. Jen musíme vědět, jak ji využít.
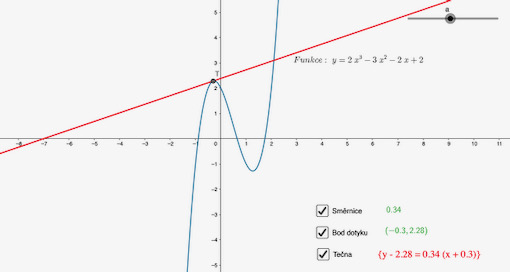
Postup práce je jednoduchý: A) nakreslíme zadanou funkci, B) vytvoříme bod T jako jeden z bodů grafu, C) zadáme derivaci funkce, D) vypočítáme směrnici tečny, E) zakreslíme tečnu. Pět kroků oživíme několika dynamickými prvky (text) a úloha je připravena k výkladu. Na podobných příkladech je skvělé, že jsou jednoduché, ucelené a snadno zpracovatelné.
Pro připomenutí: derivace v bodě určuje směrnici přímky a jde o parametr k ve vztahu y = kx + q. Je jasné, že hodnota derivace je v každém bodě jiná a tak dostáváme parádní přehled různých stavů, které mohou nastat. Díky barvám a několika dynamickým prvkům můžeme sestavit pěknou aplikaci, která může být i webová. Já jsem tečnu vyjádřil raději jako přímku určenou bodem než ve směrnicovém tvaru, protože po svých žácích chci, aby mezi různými zápisy dokázali přecházet.
>>>>>
07-11-2021