Shodné zobrazení - otáčení
Hezká středoškolská úloha stojí za vyzkoušení.
Mám jednu hodně oblíbenou konstrukční úlohu, která se řeší pomocí otáčení. Vlastně si uvědomuji, že chci, aby si ji prožili všichni moji studenti a nepřišli tak o její krásu a eleganci. Protože je dobré se k ní občas vrátit, například před maturitou, zpracoval jsem ji v Geogebře a natočil i video. To je na YouTube v odkazu pod článkem.
Jsou dány tři soustředné kružnice s poloměry r1 < r2 < r3. Sestrojte rovnostranný trojúhelník ABC tak, aby každý z jeho vrcholů byl umístěn vždy na jedné kružnici.
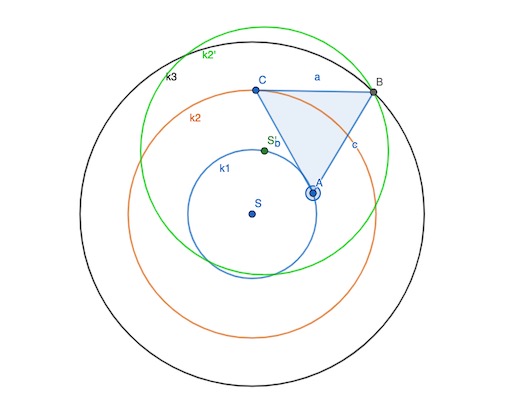
Úloha je hodně povedená a vyžaduje trochu víc než jen bezmyšlenkové copy/paste. A právě to z ní dělá ideální ukázku, jak lze aplikovat shodná zobrazení do konkrétních situací. Přidaná hodnota je v celkovém pojetí, protože jednak je třeba pochopit otáčení, jednak umět jej používat a nakonec promyslet klíčový problém - co vlastně zobrazovat a proč.
Konstrukce má ještě jeden význam. Na konci videa jsem doporučil vyhodnotit poměry poloměrů kružnic v souvislosti s možným počtem řešení. Když se hledá obecně, dokáže taky potrápit, určitě stojí za zamyšlení. K nahlédnutí na YouTube mám i další jednodušší příklad na sestrojení čtverce pomocí otáčení, ale tento je hezčí.
>>>>>
10-12-2023