Články
Fyzika v Geogebře
Dynamické modelování pohybu.
Zajímavou fyzikální úlohu můžeme vytvořit i pomocí Geogebry. Ona to je vlastně pořád matematika, neboť se jedná o pohyb rovnoměrný přímočarý, tj. o úlohu o pohybu. Nejde ale ani tak o výpočet, ale o experimentální hrátky. V podstatě bude dohánět jeden objekt druhý. A my budeme řešit otázku, jak nastavit parametry, aby oba objekty doběhly do cíle současně.
Prvnímu (běžci) určíme rychlost, klidně závislou na dalším parametru - viz posuvník b. U druhého (cyklisty) zvolíme zpoždění startu pomocí podmínky závislé na uražené vzdálenosti běžce. Jednoduchým experimentováním (změnou podmínky) se budeme snažit dosáhnout stejného okamžiku pro dosažení cíle.
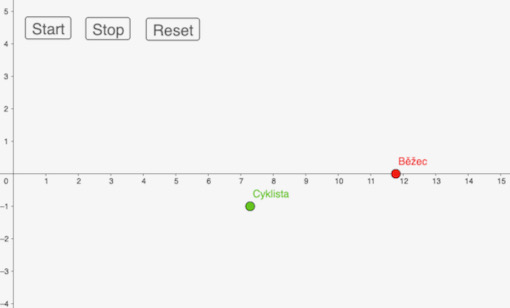
Jde opravdu o experimentální hru. Pokud ale chceme se žáky ověřit výsledek výpočtem, půjde o jednoduchou rovnici z úloh o pohybu. Příklad je o fyzice i matematice. Určitě je vhodné vést žáky k tomu, aby se snažili pochopit, co vlastně počítají.
Jak dojdeme k tomu, že cyklista vyjede, když má běžec za sebou právě 6 metrů? Celkový čas je 5 s pro dráhu 15 m. Takže zpoždění o a = 2 s (v druhé rovnici) vynásobíme 3 (jeho rychlost).
s = v.t
15 = 3x - (běžec)
15 = 5(x-a) - (cyklista)
a = (2/5).x (čas běžce, zde v sekundách)
Jestliže x=5, potom a=2)
Další možnost je v řešení úlohy grafickou metodou. To již experiment není, protože žáci pracují s lineární funkcí, resp. s grafickým řešením soustavy lineárních rovnic. Je opravdu důležité, aby pochopili rozdíl mezi modelováním úlohy a řešením. Pro obě situace používáme Geogebru, pokaždé ale s jiným cílem. Oba přístupy jsou uvedeny ve videu pod článkem (YouTube).
A to nejlepší nakonec. V experimentální úloze je nastavena rychlost běžce jako konstanta. Ale pokud ji zadáme také jako měnící se parametr (b), dostaneme další možná řešení. Ve videu jsem zvolil změnu jen v přirozených číslech, aby mohli žáci dojít k rozumným výsledkům. A v další úrovni můžeme naznačit běžci, aby na celém úseku zrychloval.
>>>>>
03-10-2021