Historie a původ fraktálů
Vztah pro výpočet dimenze
D = log N / log (1/r)
D - označení fraktální dimenze objektu
N - faktor změny délky
1/r - faktor změny měřítka
r - délka jednoho nově vzniklého dílku při rozdělení původního útvaru či jeho části
Představme si, že máme čtverec (resp. jeho obvod), ve třetině každé jeho strany vytvoříme nový čtverec (bez jedné strany - vznikne tak spojitá, lomená čára bez derivace ve všech bodech). V podstatě jsme původní délku strany
přetransformovali na 1/3 (r = 1/3) původní hodnoty, počet samopodobných úseků bude 5 (N = 5).
D = log 5 / log 3 = 1,46
Tato hodnota řadí nově vzniklý útvar někam mezi přímku (D=1) a plochu (D=2). Nově vzniklý útvar bude zřejmě neustálou transformací převeden v objekt, který bude mít ve fraktálovém pojetí nekonečný obvod a jím vymezený obrazec bude mít konečnou plochu.
L - systémy
Cantorovo diskontinuum
Vznikne postupným dělením úsečky na 3 shodné části. Prostřední vypustíme, a tak postupujeme dál. Délka "nekonečně" mnoha úseček
konvertuje k nule, ale počet bodů jde k nekonečnu.
Kochova vločka
K základnímu trojúhelníku přidáme k prostřední třetině každé strany trojúhelník o třetinu menší. Hranicí tohoto vzniklého útvaru je
lámaná křivka, která nikdy neprotne sebe sama. Plocha konvertuje ke konkrétní hodnotě, obvod je nekonečně dlouhý.
Sierpinského trojúhelník
Z trojúhelníka vyjmeme trojúhelník vytvořený středními příčkami. Toto opakujeme stále u každého nově vzniklého útvaru, až dostaneme
nekonečně mnoho trojúhelníků s plochou konvertující k nule.
Mengerova houba
Trojrozměrná mřížka, která má nekonečně velký povrch a jejíž objem konvertuje k nule.
Cantorovo diskontinuum

Sierpinského trojúhelník
Systémy iterovaných funkcí (polynomické fraktály)
Barnsleyho kapradina
Nádherný geometrický útvar, kdy se ukazuje, že každý lístek kapradiny je téměř kopií sebe sama. V podstatě vznikl tak, že původní
útvar byl postupně doplňován dalšími útvary, které byly zmenšenou kopií původního. Tyto menší útvary byly pokládány tak, že mohly i překrývat
původní objekt. Drobné zkreslení je naprosto zanedbatelné, řekl bych, že až žádoucí. Takto vzniklý útvar teprve vedl k pokusu o "zmatematizování".
Newtonova množina
Útvar vznikl grafickým řešením Newtonovy rovnice x3-1=0 v oboru komplexních čísel. Body (modely řešení) vždy v grafickém
zobrazení konvertují k určitému kořenu. Při grafickém řešení se na rozhraní ploch určujících řešení objevily další nové obrazce.
Juliova množina
Náhodně zvolené komplexní číslo c bude charakterizovat množinu. Každý bod z roviny v komplexním oboru umocníme a přičteme k němu c. V případě, že výsledné číslo konvertuje
k nule, patří do Juliovy množiny. Velmi zajímavé je zbarvení množin. Závisí totiž na na počtu iterací potřebných ke zjištění, zda číslo patří do Juliovy
množiny.
Mandelbrotova množina
Tato množina v komplexní rovině vznikne tak, že v každém svém bodě určuje vzhled Juliovy množiny. K určitému komplexnímu
číslu přičteme jeho druhou mocninu. Tento výsledek umocníme a přičteme k němu původní číslo. Pokud výsledek nepřesáhne hodnotu 2, patří bod do
množiny. Mohou zde být různé typy množin závislé na zvoleném exponentu, což
vede až k neuvěřitelně krásným útvarům. Jinými slovy, tato množina je
propojena s Juliovou množinou tak, že každý bod Mandelbrotovy množiny určuje
vzhled množiny Juliovy ve vztahu k určitému bodu. Počet iterací určuje barvu
čísla.

Barnsleyho kapradina

Newtonova množina

Juliova množina

Mandelbrotova množina
Dynamické systémy
Lorenzův atraktor
Popisuje chování vodního kola, kdy výsledkem je nekonečná křivka, která nikdy neprotne sebe sama. Připomíná motýlí křídla,
která se možná stala symbolem chaosu.
Hénonův atraktor
Vzniká neustálým natahováním a ohýbáním fázového prostoru. Přes svou jednoduchost je pro matematiky stále záhadným, neboť
jednotlivé vzniklé křivky jsou vlastně páry křivek vedle sebe. Bez výpočtu nejde určit, kde se objeví následující bod křivky.
King´s dream
Fraktál vytvořený opravdu jen pro radost.
Přírodní fraktály
Útvary vzniklé přírodní oscilací a turbulencí.
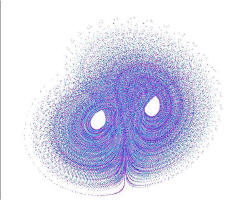
Lorenzův atraktor

Hénonův atraktor
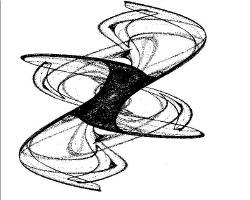
King´s dream

Orbitál (přírodní fraktál)